Надежность и долговечность машин. ВАЗ-2101
ЗАДАНИЕ 2. РАСЧЕТ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ ПРИ ИЗВЕСТНЫХ РАСПРЕДЕЛЕНИЯХ НАРАБОТКИ НА ОТКАЗ
Цель задания – расчет показателей безотказности, который является основой для количественного описания надежности машин и систем, позволяет сравнивать системы и дает логическое основание для повышения их надежности.
Долговечность контрольно-измерительных приборов автомобиля ВАЗ-2101 имеет нормальное распределение с математическим ожиданием 600 часов и среднеквадратическим отклонением 27 часов.
- Построить график плотности распределения;
- Построить график интенсивности отказов до значения t=600 часов;
- Определить значение плотности распределения втечении 430 часов;
- Сколько приборов выйдет из строя за 430 часов;
- Количество автомобилей – 90 штук.
1. График плотности распределения имеет симметричное изображение, поле рассеивания:
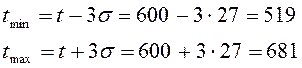
Функция распределения:
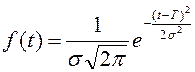
Рассчитав по этой формуле значение функции в промежуточных точках (таблица 2), построим ее график (рисунок 3).
Таблица 2.
| tmin |
tmin+
|
tmin+2
|
t |
tmax
|
tmax-
|
tmax | |
| 519 |
546 |
573 | 600 | 627 | 654 | 681 | |
| f(t) | 0,000164 | 0,002 | 0,008962 | 0,014776 | 0,008962 | 0,002 | 0,000164 |
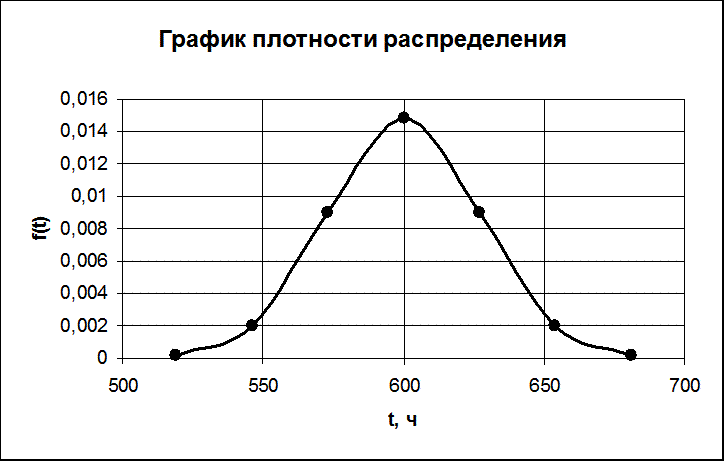
Рисунок 3 – График плотности распределения
2. Интенсивность отказов 
– условная плотность вероятности отказа невосстанавливаемого изделия определяется для данного момента времени при условии, что до этого момента отказа не было.
Интенсивность отказов рассчитывается по формуле:
,
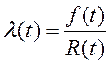где: f(t) – функция плотности вероятности отказа;
R(t) – вероятность безотказной работы:
,
F(t) – вероятность отказа:
.
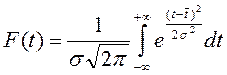Для определения F(t) используем нормированную функцию Ф(z), для нее принимаем случайную величину:
Нормированное отклонение записываем в виде:
.
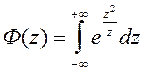Тогда имеем:
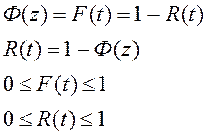
F(t)=0, Ф(z)=0, z=-3,9, t=494,7.
Результаты вычислений занесем в таблицу 3, график интенсивности отказов показан на рисунке 4.
Таблица 3.
| t | z | R(t) | f(t) |
|
| 494,7 | -3,9 | 1,0000 | 0,000007 | 0,00001 |
| 500 | -3,7037 | 0,9999 | 0,000016 | 0,00002 |
| 510 | -3,33333 | 0,9996 | 0,000057 | 0,00006 |
| 520 | -2,96296 | 0,9985 | 0,000183 | 0,00018 |
| 530 | -2,59259 | 0,9952 | 0,000513 | 0,00052 |
| 540 | -2,22222 | 0,9869 | 0,001251 | 0,00127 |
| 550 | -1,85185 | 0,9680 | 0,002660 | 0,00275 |
| 560 | -1,48148 | 0,9308 | 0,004931 | 0,00530 |
| 570 | -1,11111 | 0,8667 | 0,007970 | 0,00920 |
| 580 | -0,74074 | 0,7706 | 0,011230 | 0,01457 |
| 590 | -0,37037 | 0,6444 | 0,013796 | 0,02141 |
| 600 | 0 | 0,5000 | 0,014776 | 0,02955 |
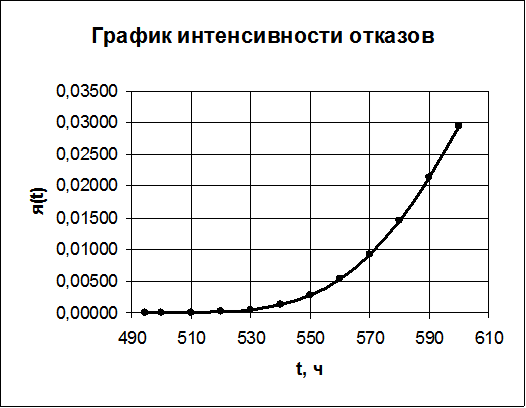
Рисунок 4 – График интенсивности отказов
3. Плотность распределения в точке t=530:
f(t)=0,000530.
4. Определить, сколько приборов выйдет из строя за t=530 часов.
Нормированное отклонение 
=-2,59259
F(t)=Ф(z)=0,004763
Определим количество приборов, вышедших из строя в интервале от 530 до 600 часов.
Вероятность отказов в интервале t1..t2:
z1=-2,59259; Ф(z1)=0,004763
z2=0; Ф(z2)=0,5
F(t)=0,495237
n=N*F(t)=90*0,495237=44,57135
Определим средний пробег в км между отказами 
:
,
где: n=320 – количество отказов;
l=150000 – срок службы;
N=42 – количество автомобилей.
Для экспоненциального закона распределения
Таблица 4.
| l, км | 0 | 15000 | 30000 | 60000 | 120000 | 150000 |
| f(l) | 19687,5 | 9211,051 | 4309,509498 | 943,3331866 | 45,20013 | 9,894114 |
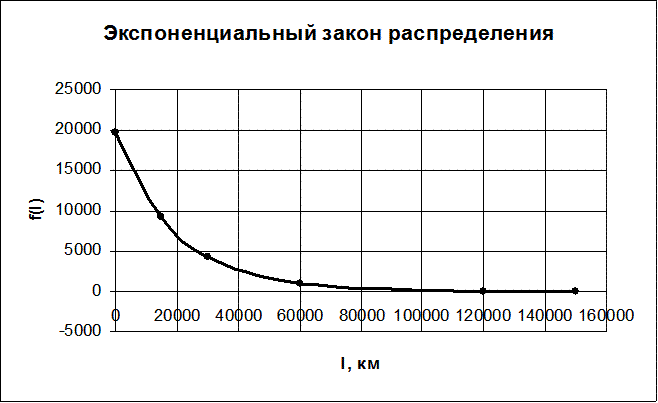
Рисунок 5 – Экспоненциальный закон распределения
Вероятность безотказной работы рассчитывается по формуле:
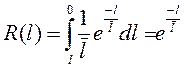
Таблица 5.
| l, км | 0 | 15000 | 30000 | 60000 | 120000 | 150000 |
| R(l) | 1 | 0,467863 | 0,218895721 | 0,047915336 | 0,002296 | 0,000503 |
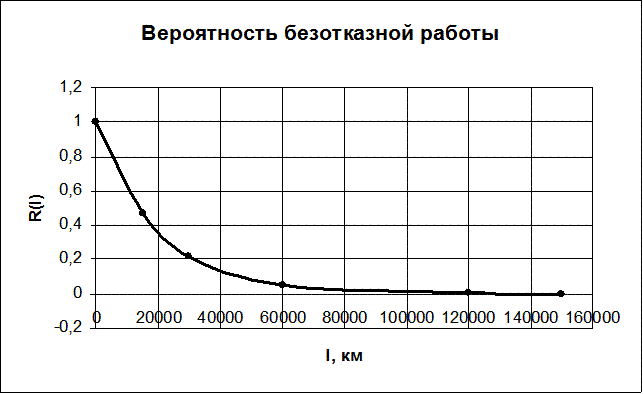
Рисунок 6 – Вероятность безотказной работы
Интенсивность отказов рассчитывается по формуле:
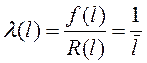= 0,00005